恒容容器放气的瞬时流量的计算与合金氢化物放氢流量曲线的计算

有时候，你会遇到一个问题，该问题的描述如下：

你有一个已知体积的容器，设容器体积为V，里面装有一定压力(初始压力)的气体，如空气或氢气等，设初始压力为1MPa，容器出口连接着一个阀门开关，开关后面接1/4in.的钢管，钢管出口即为气体出口。当阀门瞬间全开时，气体出口的瞬时流量值随时间变化到底是怎么样的呢？

该问题相当于在不考虑管壁与管长对气体产生粘滞阻力的影响下，已知气体管道直径d，即管道横截面积 $A=\frac{\pi d^{2}}{4}$ ，已知管子进口静压为 $P_0=1MPa$ ，已知管子出口静压为 $P_{b}=P_{atm}$ ，即一个大气压，同时知道进口气体总温 $T_{0}$ 为323K，求出口瞬时流量随时间 $t$ 的变化关系和曲线。

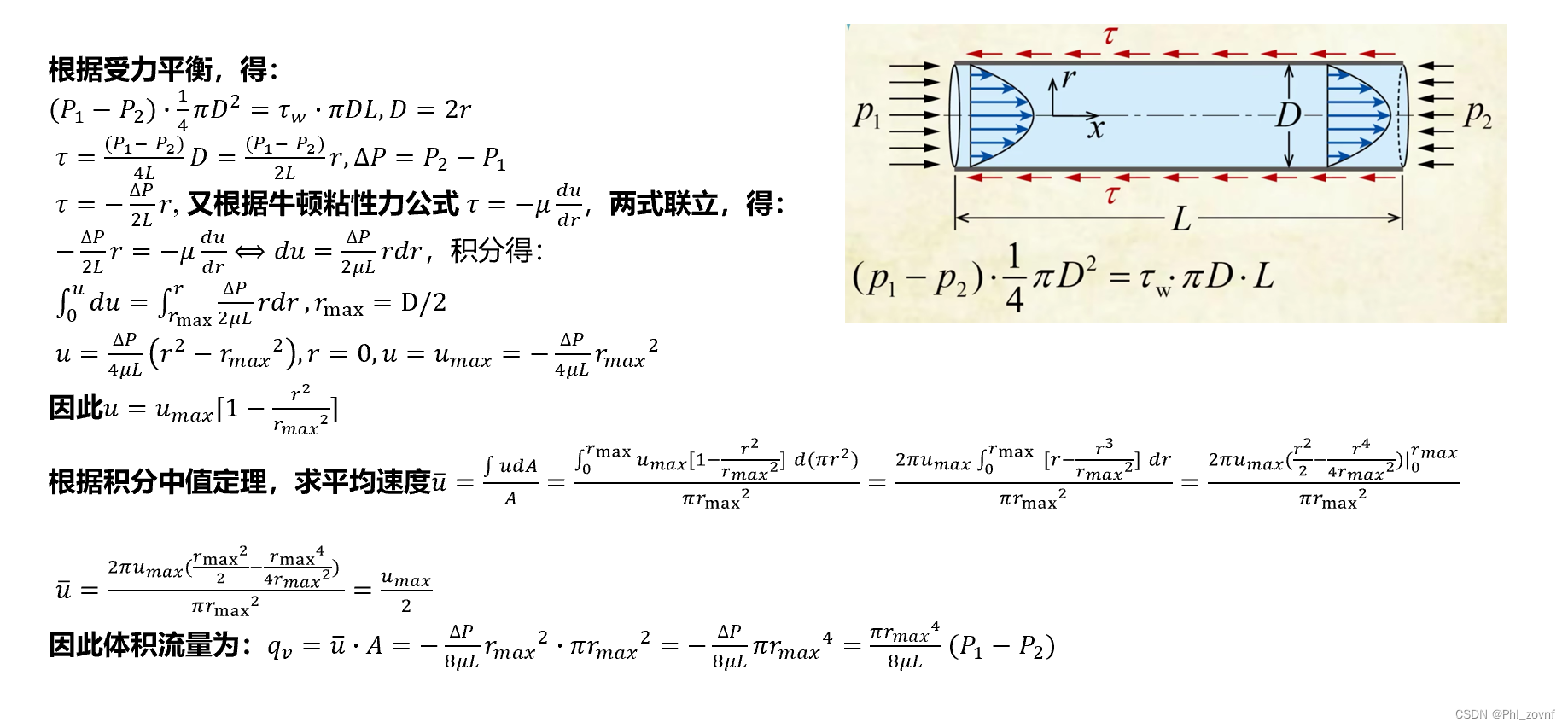
1. 第一种方法：根据哈根泊谡叶方程

利用理想气体方程： $PV=\frac{m}{M}RT$ 和哈根泊谡叶关系式： $q_v=\frac{\pi r^{4}}{8\mu L}\Delta P,\Delta P=P-P_{atm}$ ， $q_v$ 表示的是体积流量，单位为 $m^{3}/s$ ， $r$ 是管子的半径， $\mu$ 是流体的动力黏度，单位是 $kg/(m\cdot s)$ ， $L$ 是管子的长度，压强 $P$ 的单位为 $Pa$ 。两个方程联立，可得 $ln(\frac{P-P_{atm}}{P_0-P_{atm}})=-ABt,A=\frac{\pi r^{4}}{8\mu L},B=\frac{\rho RT}{MV}$ ， $P-P_{atm}=(P_0-P_{atm})e^{-ABt}$ ，利用该关系式，得到 $P$ 随时间 $t$ 的关系如下图所示，为一指数函数形式，而且可以通过积分，得到积分总流量为 $7.45L$ ，根据 $\Delta PV=\Delta mR_gT,\Delta m=\frac{\Delta PV}{R_gT}\Leftrightarrow \Delta q=\frac{\Delta m}{\rho }=\frac{\Delta PV}{\rho R_gT}=7.46L$ ，可见积分与差分得出的总流量非常接近。

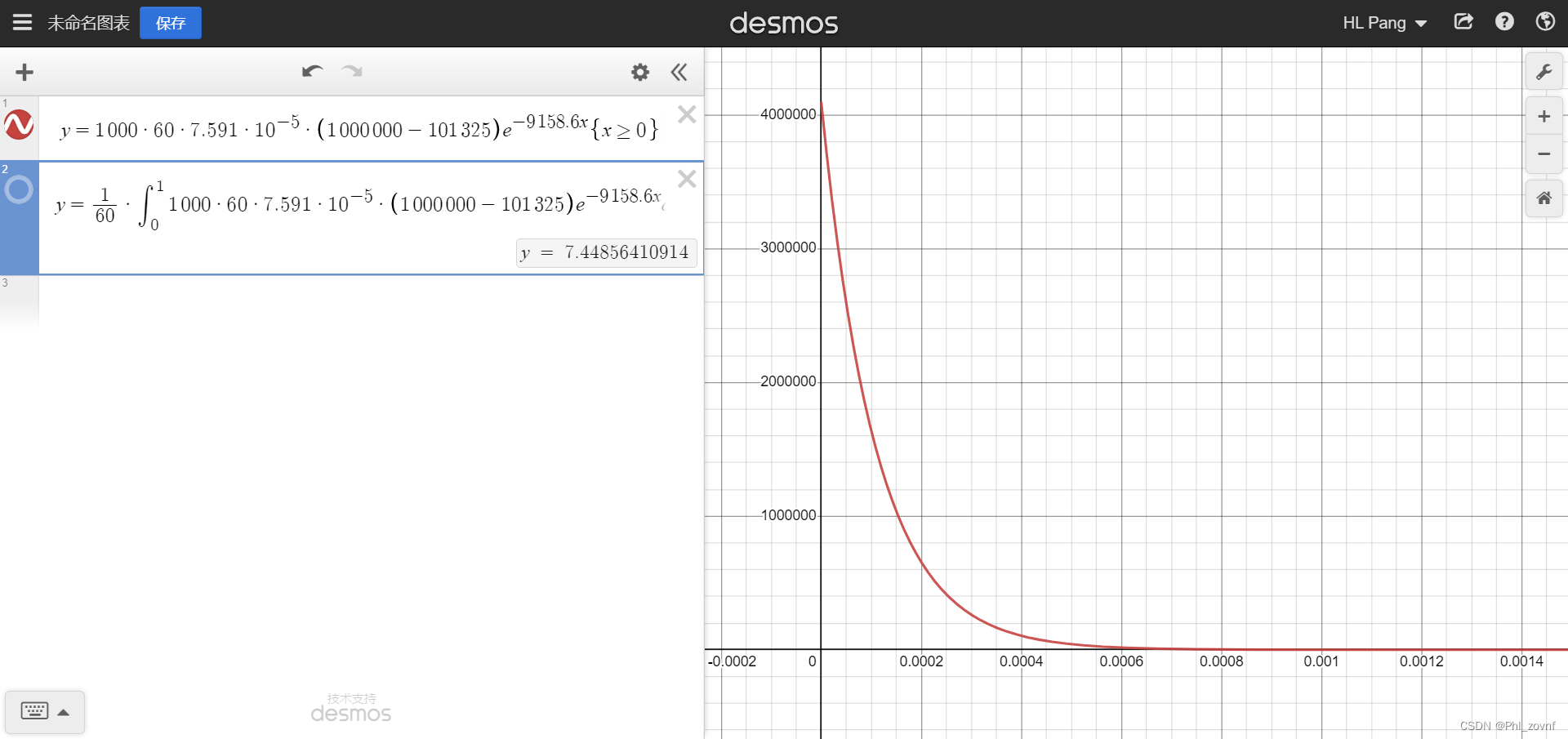
不过根据推导，一开始的瞬时流量值非常离谱，可以去到 $4093105SLM(L/min)$ ，根据 $\frac{dm}{dt}=\rho \cdot u\cdot A\Leftrightarrow \frac{dq}{dt}=\frac{d(m/\rho )}{dt}=u\cdot A$ ， $A=3.167\times10^{-5} m^{2}$ 可以知道出口流体平均速度 $u=4093105\cdot 10^{-3}/60/(3.16\times10^{-5} )=2154092m/s$ ，光速是 $u_c=299792458m/s$ ，出口速度已经达到 $0.007$ 倍的光速，也超过空气声速 $\approx 314m/s$ ，应该会听到音爆？实际好像没有发生这样的现象，但出口处确实会产生挺大的声音。

附：关于哈根泊谡叶关系式的推导，见下图。

2. 第二种方法：根据气体动力学推算

假设排气过程与气体管道壁面的换热忽略不计，即壁面是绝热的，气体流体是一个准稳态问题，排气口相当于是收缩，没有扩张，根据气体动力学可知，出口气体流速只能加速到1马赫数，即 $Ma=1$ 。根据总静温关系式 $\frac{T_{0}}{T_{b}}=1+\frac{k-1}{2}Ma^{2},T_0=323K$ ，得知 $T_b\approx 269.17K$ 。再根据马赫数定义式 $Ma^{2}=\frac{v^{2}}{c^{2}}=\frac{v^{2}}{kR_gT}$ ，这里 $k$ 是气体比热容比，定义为定压比热 $C_p$ 与定容比热 $C_v$ 之比，变换后有 $v_b=Ma\cdot \sqrt{kR_gT_b}$ ， $k=1.4$ ， $T_b=269.17K$ ，比气体常数 $R_g$ 为： $R_g=\frac{R=8.314J/(mol\cdot K)}{0.002kg/mol}=4157J/(kg\cdot K)$ ，得到氢气气体流速 $v_b\approx 1295.22m/s$ 。

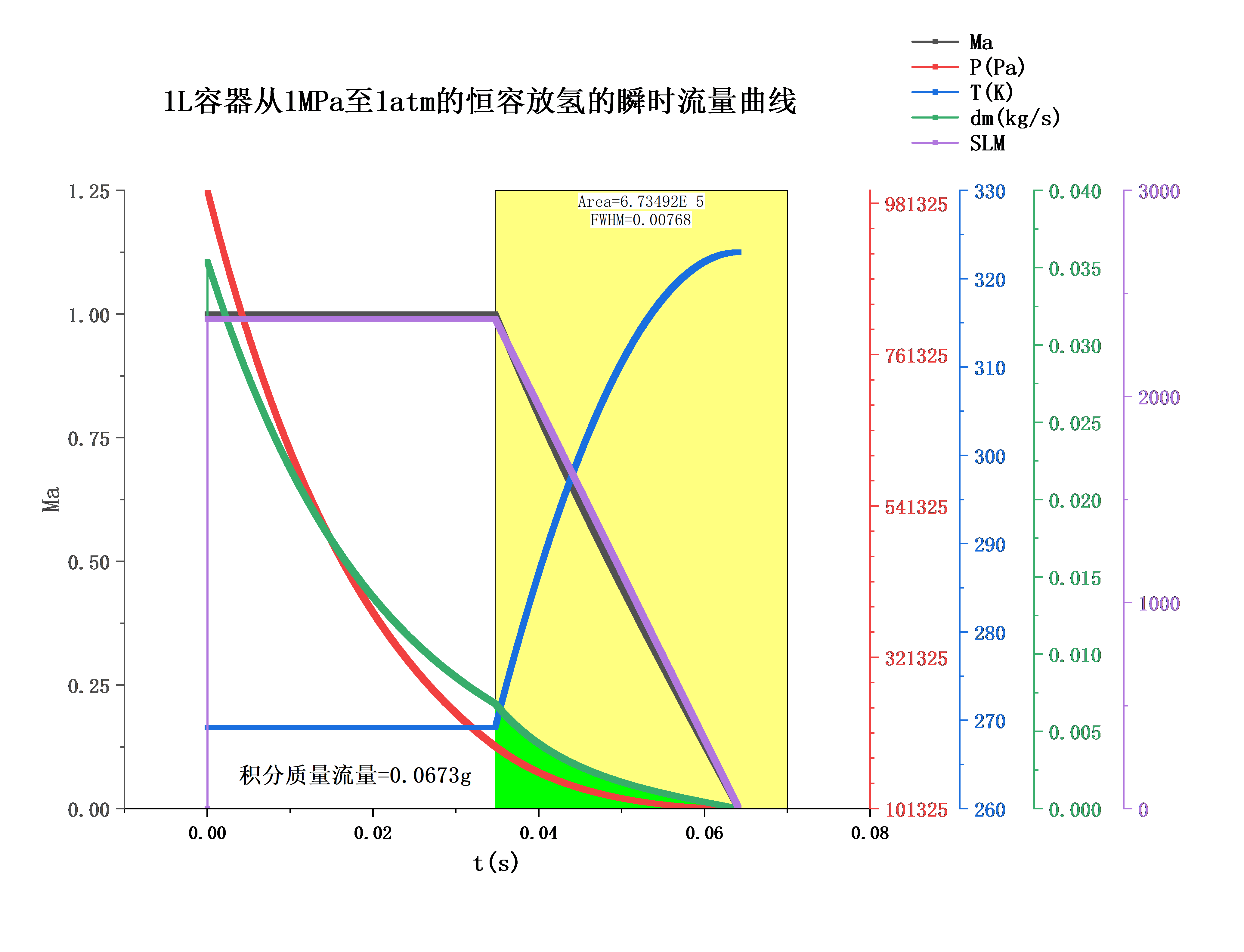
根据 $\frac{dm}{dt}=\rho \cdot u\cdot A$ ， $P=\rho R_gT$ , $\frac{T_{0}}{T_{b}}=1+\frac{k-1}{2}Ma^{2},T_0=323K$ ， $Ma=1$ ， $\frac{P}{P_b}=(1+\frac{k-1}{2}Ma^{2})^{\frac{k}{k-1}}$ ， $u=Ma\cdot \sqrt{kR_gT_b}$ ， $P_{b}$ 为一个大气压。在 $Ma=1$ 的壅塞流阶段，可解得 $ln\frac{P}{P_0}=\frac{\sqrt{1.2kR_gT_0}}{V}MaAt\Leftrightarrow P=f(t)=P_0e^{-47.734t}$ 。这阶段，理解为流速 $u$ 不变， $P$ 变化导致的 $\rho$ 变化，瞬时质量流量也会随之变化，但体积流量 $q_v=u\cdot A$ 不变。如下图所示，绿色曲线是瞬时流量，紫色曲线是体积流量，绿色部分面积是积分得到的总质量流量，通过积分得到壅塞流下的总质量流量为 $0.602g$ ，换算成密度为 $0.0899kg/m^{3}$ 的体积流量为 $6.69L$ 。

后面非壅塞流状态下的亚声速流，原则上也是利用 $\frac{dm}{dt}=\rho \cdot u\cdot A$ ， $P=\rho R_gT_b$ ， $u=Ma\cdot \sqrt{kR_gT_b}$ ， $\frac{T_{0}}{T_{b}}=1+\frac{k-1}{2}Ma^{2},T_0=323K$ ， $\frac{P}{P_b}=(1+\frac{k-1}{2}Ma^{2})^{\frac{k}{k-1}}$ ，这5个式子得到 $\frac{dm}{dt}=f(P)$ 的关系，我用欧拉法获得解析解的近似值，得到后续的流量曲线，具体步骤是，知道压力初始条件 $P=P_{Ma=1}\approx 191801Pa$ ，初始瞬时流量为 $\frac{dm}{dt}|_{Ma=1,P=P_{Ma=1}}$ ，也就是等于壅塞流状态下最后一刻时间的流量，然后利用瞬时流量乘以时间小量，得到 $\Delta m$ ，再利用关系式 $\frac{dm}{dt}=f(P)$ ，得到 $P$ 的变化量，然后计算马赫数 $Ma$ 、速度 $u$ ，温度 $T_b$ 等参数，不断进行迭代计算，当 $P/P_{b}\approx 1$ 时结束迭代。如下图中绿色的质量流量曲线和紫色的体积流量曲线，通过积分面积算得亚声速流下总质量流量为 $0.0673g$ ，换算成密度为 $0.0899kg/m^{3}$ 的体积流量为 $0.749L$ ，因此放氢整个过程总质量流量为 $0.602g+0.067g=0.669g$ ，与 $\Delta PV=\Delta mR_gT,\Delta m=\frac{\Delta PV}{R_gT}\Leftrightarrow \Delta m=0.669g$ 算出来的基本一致。整个过程的总体积流量为 $6.69L+0.749L\approx 7.44L$ 。

具体更可靠的计算，请读者参考GB/T 14513.3-2020中的方法。

在经典的合金氢化物动力学描述中，有一种是用JMAK方程来描述和拟合合金的吸放氢过程，方程很简洁： $\xi =1-e^{-kt}$ ，其中 $\xi$ 是反应程度或者百分比，表示合金氢化物吸氢或者放氢的程度， $k$ 是该合金吸氢或放氢的一种特征常数，经常是通过实验测得动力学曲线后进行拟合得到， $t$ 是时间。该方程的曲线形状如下图所示。

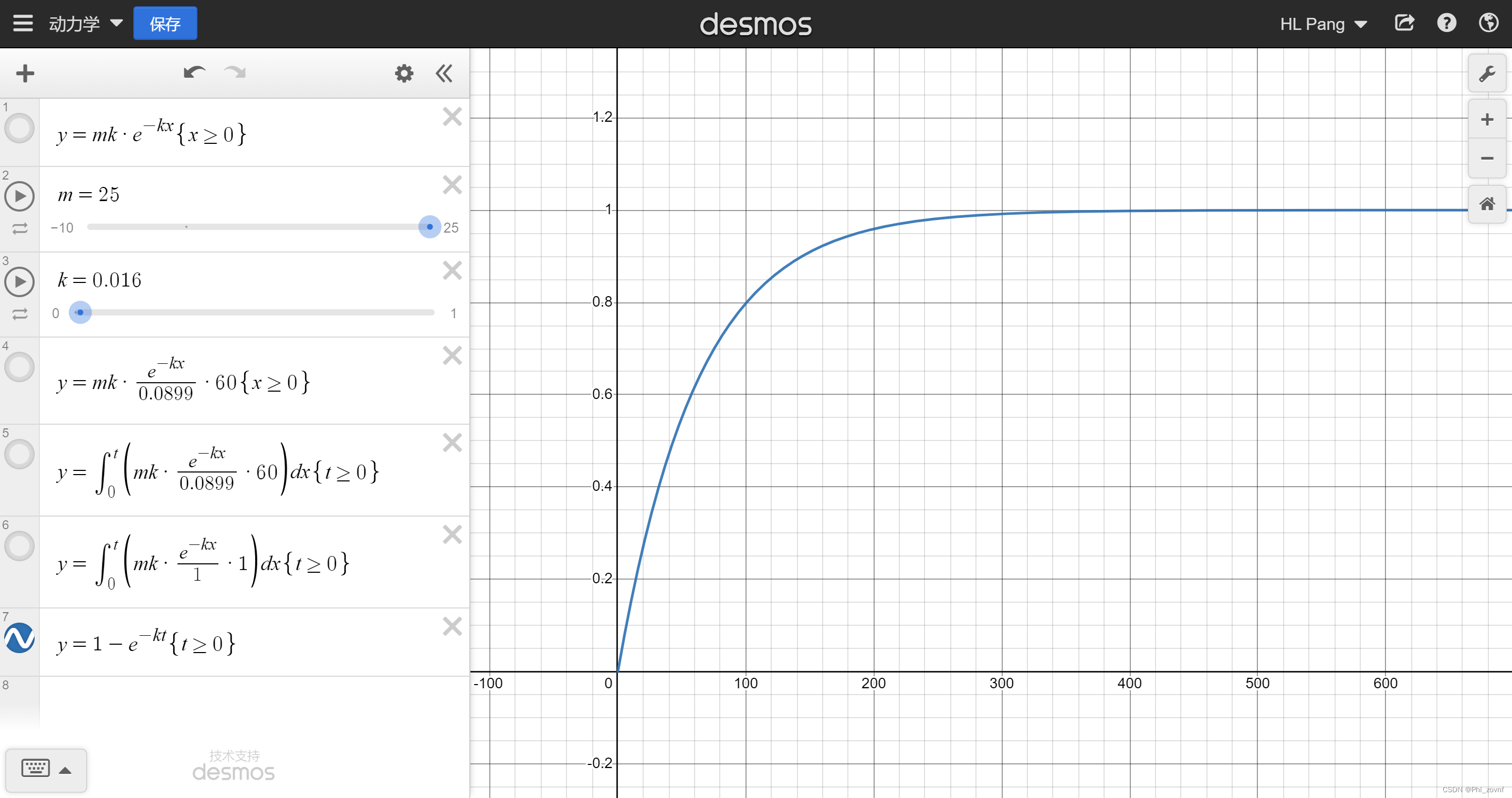
由于 $\xi$ 是反应程度，因此假设合金最终能放出 $m$ 标升的氢气，则方程可变为 $q_v =m(1-e^{-kt})$ ，该方程对时间 $t$ 进行求导，可得 $\frac{dq_v}{dt}=mke^{-kt}$ ，该曲线即为瞬时体积流量曲线，其曲线形状如下图， $k$ 越大，初始瞬时流量越大，放氢时间越短。 $k$ 实测可取值0.00005~0.05之间。

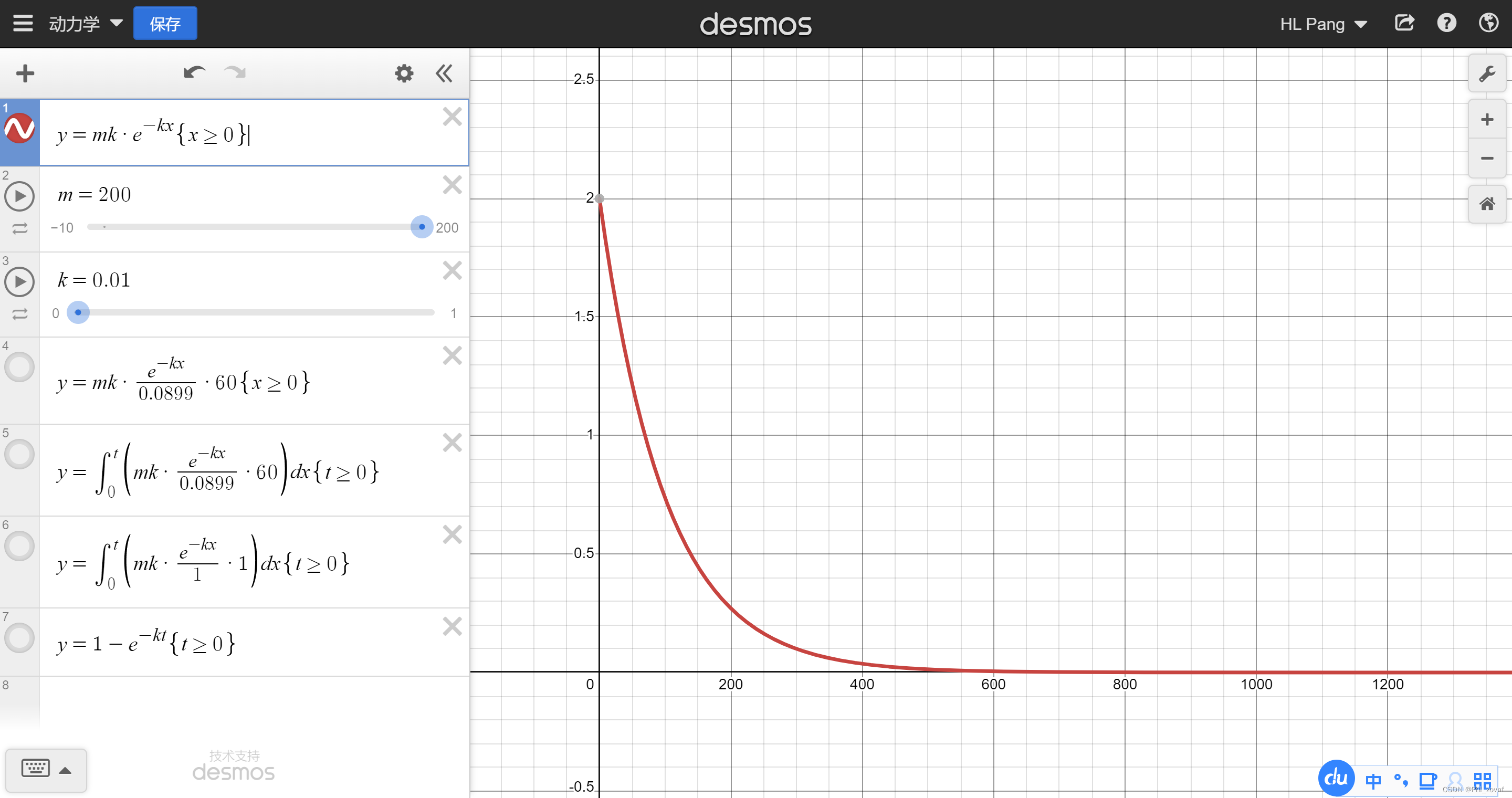
合金放氢后，使得容器内压力 $P$ 上升，合金动力学方程 $q_m =m(1-e^{-kt})$ ， $m$ 是放氢总质量，在这里，我假设 $m=0.2g, k=0.02$ ，利用上述5个公式和数值计算，可以知道在壅塞流状态下，合金动力学方程中，每 $10^{-5}s$ 放出的氢，导致容器内上升的压力只有 $0.55Pa$ 左右，结合上述气体动力学算出来的瞬时流量，可认为这阶段合金放氢所带来的压力影响可忽略。就算是非壅塞流阶段，由于合金总储氢量 $m$ 比较小，因此也是接近非壅塞流末段，合金放氢对瞬时流量的影响才开始凸现，此时合金单独放氢的动力学曲线此时可以接驳到瞬时流量曲线上去。也就是说，瞬时流量曲线前部分是气体动力学算出来的流量曲线，到一定压力时，合金放氢动力学曲线就跟前者流量曲线接上即可。

我大概算了下，通过数值计算的瞬时流量如下图，10s的瞬时流量为26.97SLM(L/min)，20s的瞬时流量为22.08SLM，30s的瞬时流量为18.08SLM，50s的瞬时流量为12.12SLM，100s的瞬时流量为4.46SLM， $\frac{dq_v}{dt}=mke^{-kt}/\rho$ 算出来10s的瞬时流量为26.06SLM，20s的瞬时流量为21.31SLM，30s的瞬时流量为17.45SLM，50s的瞬时流量为11.69SLM，100s的瞬时流量为4.30SLM。两者算出的差距是有，但不算特别大，可接受。